欧洲图形绘制研讨会文献：在粗糙表面上折射的微表面模型(Microfacet Models for Refraction through Rough Surfaces) (附：原文下载)

前言

Microfacet Models for Refraction through Rough Surfaces

在粗糙表面上折射的微表面模型

作者：Bruce Walter 、stephen R. Marschner 、Hongsong Li 、Kenneth E. Torrance

计算机图形学专业：康奈尔(Cornell)大学、北京理工大学

文章编辑：Jan Kautz 、 Sumanta Pattanaik 译制：R 站(btbat.com)

反正你也学不会系列，本文献对微表面模型做了一些综述，极具参考价值，因为来自 Arnold 官方推荐，其中包含一些微表面理论、GGX、Phong 和 Beckmann 分布函数、反射、折射、采样、Smith 阴影等函数的实现、测量、推导过程等等，希望能提高大家对原理性的了解，并提供一些参考性作用，另一方面了解下大佬的研究方法和态度！由于涉及诸多术语和公式，翻译可能有不对之处，欢迎多多指正，太蛋疼了。

摘要

微表面(Microfacet)模型，被用来建模光在粗糙表面上反射，已经被证明是非常成功的，在本文中，窝萌将回顾微表面理论，并演示如何将其模拟并扩展到，在粗糙表面上透射(Transmission)(如蚀刻玻璃)。我们将从透射模型与几个真实曲面中得到的实测数据进行了比较，并讨论了微表面分布和阴影遮蔽函数的适配选择。由于渲染透射介质，至少需要追踪 2 个接口的光，因此良好的重要性采样，是实操的必要条件。因此，我们也描述了采样微表面模型的有效方法，和相应的密度概率函数。

类别和主题描述符(根据 ACM CCS):I.3.7[三维图形和真实感]

关键词:折射(Refraction)、微表面 BTDF、 Cook-Torrance 光照模型、全局光照(Global lIllumination)、蒙特卡罗采样(Monte Carlo Sampling)

1、介绍

在许多材质效果中，射入或通过折射介质，也就是透射是材质的一个重要的组成部分，主要是指透明的物质，如玻璃、水、半透明的物质、如皮肤、大理石...当物质边界光滑时，利用斯涅尔(Snell's Law)折射定律可以很容易的模拟透射，然而当边界比较粗糙时，则缺乏用于计算机图形学的、基于物理的、经过验证的模型。

本文我们首先回顾微表面理论，并展示如何使用半向量泛化(指模型很好地拟合以前未见过的新数据(从用于创建该模型的同一分布中抽取)的能力?)，来模拟介质之间粗糙边界处的反射和折射，这提供了一个完成的 BSDF 模型分析，可以用来模拟粗糙的透射材质，如图 1 所示的蚀刻玻璃球。我们的目标之一是为玩家提供一个完整的、自洽的参考，因此我们提供了所有必要的公式，并讨论一些实际的问题，比如分布的选择、阴影遮蔽、重要性采样。由于透射光必须且至少会交叉 2 个接口，因此良好的重要性采样，对于高效渲染至关重要。

图 1：使用我们的微表面折射模型(粗糙度由纹理控制，基于贝克曼(Beckmann)分布)，用世界地图蚀刻的玻璃球进行模拟。

通过对四个真实曲面透射数据的比较，验证了该模型的有效性。粗糙透射显示了几个有趣的行为(如图 2 所示)，如峰值从光滑折射方向先掠射角的强烈偏移(类似于粗糙反射中的非镜面反射峰值)，而微表面模型能够成功的预测这种效应。我们还引入了一个新的微表面分布，称之为 GGX，它比标准的 Beckmann 分布函数更适用于我们的一些曲面。

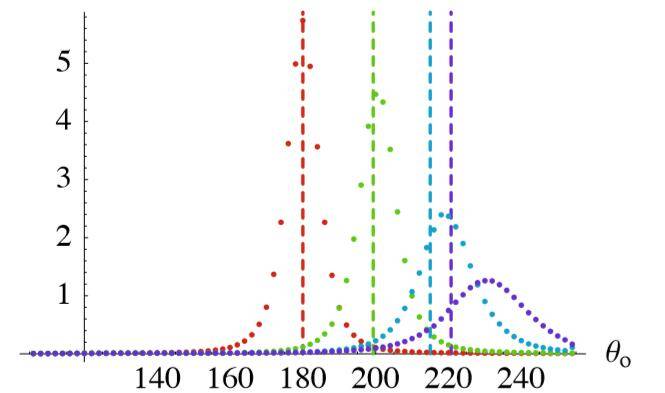
测量透射θ_i=0，30，60，80°

图 2：粗糙表面(磨砂玻璃)在 0，30，60，80°入射角的测量透射 (f_t(i,o,n) |o·n|)，虚线是由斯涅尔定律预测的光滑表面的折射方向。注意，透射波瓣(lobe)随着入射角的增加而变宽，相对于通过光滑表面的折射，透射波瓣明显的向掠入射方向移动。

微表面理论见第三部分，第四部分给出了微表面(光滑)反射和折射的适当表达式，然后第五部分给出了粗糙表面反射和折射模型，并讨论了微表面分布的选择和相关函数。第六部分描述了我们使用的测量仪器，并将我们的测量结果与拟合的微表面模型进行比较。附录 A 回顾了任意微表面分布的史密斯(Smith)阴影遮蔽近似。

2、过往大佬门的努力

Cook 和 Torrance [CT82]在光学[TS67]早期工作的基础上，将微表面模型引入图形中，用于模拟粗糙表面的光反射，而现在已经提出了许多变化(例如:，[vSK98, KSK01, PK02])。微表面模型在图形学中得到了广泛的应用，并在许多真实曲面的建模中被证明是有效的[NDM05]。

Ward [Lar92]介绍了 Cook-Torrance 模型的简化版本，并将其扩展到各向异性的反射材质。他还介绍了一种对他的模型进行采样的方法，以及贝克曼分布的一般情况，但要获得正确的采样权重，请参见[Wal05]。Lawrence 等人[LRR04]提出了一种使用拟合可分近似的采样替代方法。

Schlick [Sch94]使用理性近似为 Cook-Torrance 模型创建了一个更节省资源的近似，包括对菲涅耳公式的广泛采用的近似。

Ashikhmin 和 Shirley [AS00]提出了一种利用包含正确重要性采样的 Phong 微面分布的各向异性反射模型。[APS00]从任意的微面分布创建了能量守恒的反射模型，尽管这个公式涉及到，在没有封闭形式解的情况下，对积分进行数值估算。

与我们最接近的工作是 Stam [Sta01]，他推导了折射的微表面模型，也是作为皮肤反射率分层模型的一部分，他还推导了折射的雅可比(Jacobian)矩阵。然而，与目前的工作不同的是，Stam 没有提供重要性的采样或用实验数据验证他的模型。他还省略了阴影遮蔽术语，并使用了一个非标准的贝克曼分布变体。

提出了阴影-掩蔽项的许多近似方法(例如[TS67, San69, APS00])。我们使用 Smith [Smi67]的近似，该近似最初用于高斯曲面，后来推广到任意微表面分布[Bro80, BBS02]。

提出了基于波光学的反射模型(例如[HTSG91])，可以模拟比微表面模型更大范围的表面效应，但它们的评估要昂贵得多，并且缺乏良好的重要性采样。

还对各种粗糙表面模型的透射率进行了数值模拟，并与实测结果进行了比较[RE75, Ger03, SN91, NSSD90]。

图 3：符号元素表格

符号说明：在这项工作中，我们将使用黑体小写字母(例如：i 或 v)表示单位向量或方向。非标准化向量将用箭头(例如 h)表示，以便清楚地区分它们。有时我们会用球极坐标来描述方向(例如，v=(0v,9v))。极坐标角 e 始终是方向与宏观表面法线 n 之间的夹角，而方位角 o 则来自于垂直于 n 的某个正则方向(对于我们讨论的各向同性情况，可以任意选择该方向)。虽然我们用辐照度(即光流 light flow)来描述 BSDF(即当处理对偶时，方程是相同的(即从摄像机追踪[Vea96])。

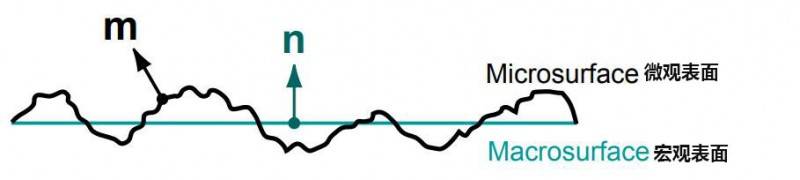
图 4：宏观表面和微观表面

3、微表面(Microfacet)理论

6.测量

为了验证我们的散射模型，我们测量了几种不同类型的粗糙玻璃表面的透射率，这种测量不能简单地通过照亮一块表面粗糙的玻璃，并测量散射光来实现，因为光线不能在玻璃内部直接观察到，而且内部反射将阻止散射到相对掠射方向的光，逃逸到可以测量的地方，同时，大量的内部反射光会从内部重新照亮粗糙的表面，产生不可接受的杂散光。

为了直接观察透射光，我们将近半球的平凸透镜，固定在采样背面，从而消除了第二个接口(图 9)。这种结构的灵感来自于[NN04]的工作。从粗糙表面照亮采样，从一定角度观察球面，仪器的旋转中心与球面中心对齐，使观察方向始终垂直于球面，通过这种方式，由于菲涅耳反射，散射光以最小的损失离开表面。此外，因为半球外的反射路径几乎垂直于表面，反射回采样中心附近区域的光相对较少，与平面采样相比，这大大减少了杂散光问题。

在我们的设置中，一个 100mm 的正方形样品，用指数匹配的粘合剂与一个直径 75mm，焦距 75mm 的平面凸透镜(近半球)粘合在一起。(所有样品均为钠钙玻璃(假设为商业样品)折射率在 1.51 左右。球形透镜为 BK7 光学玻璃，折射率为 1.52，固化胶折射率为 1.50。在我们测量的角度范围内，折射率的微小差异，会产生微不足道的反射。)对于厚度约为 6mm 的样品，透镜球面的中心位于粗糙表面上。然而，我们的样品是不同厚度的，因此该方法必须允许表面和中心之间有几毫米的距离。

样品由一个 6 毫米圆形光纤导光板的末端，从粗糙的一侧照亮，距离为 610mm(照明立体角:0.000076 sr)，光源是直流调节光纤照明器，在整个样品表面提供稳定和无闪烁的照明。透射光由冷却的 CCD 摄像机，以 f/5.6（接收立体角:0.000039 sr），通过 35 毫米镜头成像，再从半球一侧，885 毫米的距离观察样品。测量是通过平均摄像机图像中与固定矩形中的像素值来进行的，该矩形对应于球面上的面积约为 3mmx10mm。(为了保证信号在测量区域内相对恒定，对扩散较小的样品，采用较小的区域。)

由于被测区域是由图像中的固定区域定义的，所以测量值与相机所观察到的辐射率成正比。由于在折射作用下，辐射保持不变(直到一个常数因子)，这种排列产生的信号，与 BTDF 乘以入射角余弦成比例。重要的是要从前面照亮，从后面看，才有这样的特性，如果样品从半球面泛光照亮的，透镜会将光线聚焦成不均匀的辐照度分布，这将使系统对球体中心和表面之间的精确对齐变得非常敏感。

我们对四种不同工艺、粗糙表面的玻璃样品进行了测试。一种是商业生产的磨砂玻璃，由 120 号磨料（磨砂，1/16 英寸厚）的喷砂碱玻璃制成。在我们的实验室中，通过酸蚀一块钠钙玻璃板（蚀刻，3/16 英寸厚）的一侧来制备一个样品。最后两个没有那么好的特点：商用磨砂玻璃（磨砂，1/8 英寸厚），和商用可用的用于相框的防眩光玻璃（防眩光，1/16 英寸厚），除了两面粗糙的防眩光玻璃外，所有样品背面的抛光面均为平面，我们假设粘接剂填满了表面，所以额外粗糙的界面是不相关的(事实上，没有明显的证据表明空气层存在)。

测量结果一致表明，散射波瓣的峰值，明显偏离了预期的折射方向。当粗糙度较低时，如在防眩光玻璃中，峰值接近理想的折射角，但对于较粗糙的样品，峰值基本上向掠入射方向偏移。

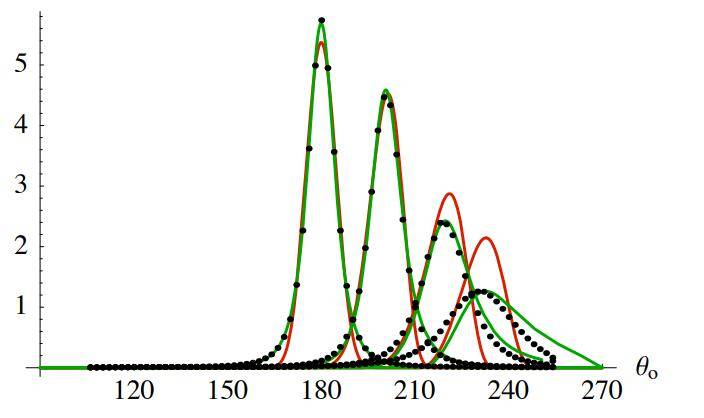
测量数据与模型 Θ_i=0, 30, 60, 80°

相对分布 D(m):数据与拟合

图 10:磨砂玻璃样品。顶部为 BTDF 拟合，底部为以实验为依据的微表面分布 D 拟合。红线为 Beckmann 拟合，绿线为 GGX 拟合。

由于这个原因，在平板上很难直接观察到，这些粗糙表面 BTDFs 的许多特征，正如我们接下来展示的，我们的微观模型很好地预测了这种行为。

6.1 采样结果

对于我们的四个采样，我们分别使用 Beckmann 和 GGX 分布，将微表面 BTDF 拟合到我们测量法线入射透射数据中(见图 12)。对于所有样本，我们假设折射率为 1.51，这为我们提供了两个要拟合的自由参数:分布宽度参数(α_b或α_g)和一个整体比例因子，以将我们的测量结果映射到绝对比例。

为了测试我们的 BTDF 模型，我们为每个示例显示了两个图，第一个表示 f_t(i,o,n)|o · n| 是透射角θ_o的函数，我们展示了进行拟合的法线入射情况(θ_i=0)，和另外三个入射角度(θ_i=30、60、80°)，以测试推断模型上这些角度。

第二幅图直接从数据中估计出微面分布函数 D 中的点，由于 G 项除掠射角外都接近 1，如果我们只使用远离掠射角的数据点(即|i·n| > 0.5 和|o·n| > 0.5)，假设 G(i,o,m) = 1 对于这些点，我们可以解出方程 21 对应的 D(h_t)值。我们也排除了测量值很低的点，因为这些点很容易受到杂散光的影响，如果数据符合一个微表面模型，这些点都应位于曲线附近，即曲面的微表面分布函数。注意，在这两个图中，模型都是由拟合的比例因子缩放的，以便与相对测量数据进行比较。

测量数据与模型 Θ_i=0, 30, 60, 80°

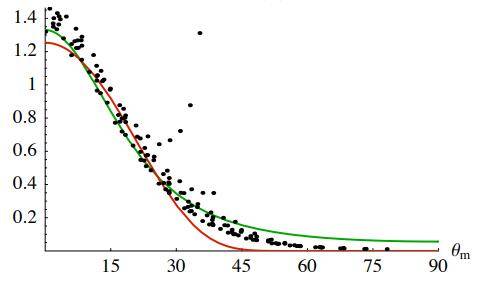
相对分布 D(m):数据与拟合

图 11:磨砂玻璃采样。顶部为 BTDF 拟合，底部以实验为依据的微面分布 D 拟合。红线为 Beckmann 拟合，绿色为 GGX 拟合。

磨砂玻璃采样的数据和模型如图 10 所示。我们可以看到 GGX 分布对数据提供了很好的拟合，比 Beckmann 拟合更接近。唯一显著的差异发生在近掠角，其中几何光学和单此散射的微表面假设可能不太有效。在发现 Beckmann 分布，与图中所示的推断的微面分布不匹配之后，我们专门开发了 GGX 分布来拟合该采样。

图 12：四个样本的拟合系数。我们使用 Beckmann 和 GGX 微表面分布，将法线入射的测量数据拟合到我们的 BTDF。在每种情况下，我们都匹配分布宽度参数，和整体比例因子（因为我们有相对的，而不是绝对的测量）。

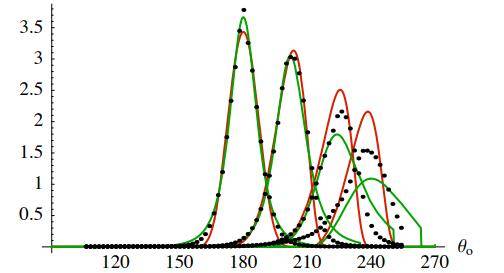
测量数据与模型 Θ_i=0, 30, 60, 80°

相对分布 D(m):数据与拟合

图 13：蚀刻采样，顶部为 BTDF 拟合，底部以实验为依据的微面分布 D 拟合。红线为 Beckmann 拟合，绿色为 GGX 拟合。

磨砂玻璃和蚀刻玻璃样品的图，如图 11 和图 13 所示。对于这两个样本，Beckmann 拟合和 GGX 拟合，都能很好地匹配测量到的透射模式，但都不能很好地匹配图 14 所示的，以实验为依据的微表面分布函数。最有可能的是，我们可以找到，介于 Beckmann 和 GGX 之间的行为分布函数，从而得到更好的匹配。

测量数据与模型 Θ_i=0, 30, 60, 80°

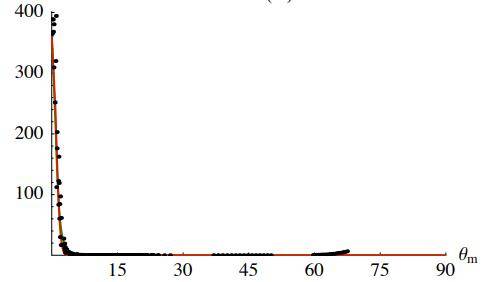
相对分布 D(m):数据与拟合

图 14:防眩光采样，顶部为 BTDF 拟合，底部以实验为依据的微面分布 D 拟合。红线为 Beckmann 拟合，绿色为 GGX 拟合。

如图 14 所示，防眩光玻璃的表面粗糙度比其他样品要低得多，因此波瓣要窄得多，因为它很窄，我们在波瓣内得到的采样相对较少，估算它的宽度也比较困难，在这种情况下，Beckmann 拟合和 GGX 拟合表现同样出色。

图 15:使用从防眩光、地面和蚀刻玻璃采样中得到的拟合分布，模拟一个表面粗糙的矩形玻璃。

利用我们的 BTDF 模型和采样技术，我们对图 15 中的防眩光、地面和蚀刻样品进行了模拟。这些图像很好地复制了它们的不同外观，以及它们模糊图案和漫反射光线的能力。图形蚀刻玻璃球的模拟如图 1 所示。

7. 结论

本文对微表面(Microfacet)论进行了全面的综述，并介绍了如何将微表面理论应用到，处理具有粗糙表面的透射材料中。

我们用实测数据验证了所得到的 BTDF 模型，结果表明该模型能够预测真实表面的折射行为。

我们开发了一种新的微表面分布函数(GGX 分布)，并表明至少在某些表面上，它比标准 Beckmann 分布更接近于测量数据。。

我们还描述了，如何有效地对微表面模型进行重要的采样，这在渲染透射光时至关重要。

我们相信，这些技术在模拟更广泛的材质方面是有用的，包括改进的半透明材质模型，如皮肤、大理石和油漆。

鸣谢： 这项工作得到了国家自然科学基金会(NSF)、ACI-0205438、CNS-0615240、CAREER CCF0347303、Alfred P. Sloan 研究基金和英特尔的支持。

附录 A：推导 Smith 阴影遮蔽, G₁

本附录简要的回顾一下，从微表面分布 D 推导出的 Smith 阴影函数 G₁;

有关详细信息，请参阅参考资料。Smith G1 最初是为高斯随机曲面创建的[Smi67]，现已推广到其他微表面分布[Bro80,BBS02]。假设我们可以将微表面表示为，相对于宏观表面的随机高度场，其特征是两种概率分布：p₁（ξ）表示高度ξ，p₂₂（p,q）表示微表面二维坡度 p 和 q，分别垂直和平行于入射面测量。p₁可以是任何概率函数，而不改变结果。二维坡度概率 p₂₂可以用以下关系式由 d 计算得出：(42)

其中余弦因子是由于测量值(立体角与坡度)的变化和和投影到宏观表面引起的。对贝克曼分布来说,这很容易证明(使用 tan²θm = p² + q²关系)，p₂₂只是一个只是标准的二维高斯分布。坡度 q 在入射面 P₂中的一维分布为:(43)

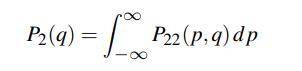
设 s(ξ₀,μ)为微表面上一个高度，为ξ₀的随机点从 V 方向可见的概率，其中μ为可见光的坡度（见图 16）：(44)

用射线在宏观表面上的投影距离τ来参数化射线，射线在τ处的高度为ξ₀+µτ。设 g(τ)∆τ为先前未被遮挡的射线，在间隔内首先与微表面相交的分数 [τ, τ+∆τ]，因此：(45)

其中 g 的作用类似于体积渲染中的衰减系数。为了计算 g，我们假设表面高度和坡度分布是独立的，g 可以近似为：从表面上方的间隔开始的光线中，有多少部分位于表面末端的下方（因此与表面相交的位置为[τ, τ+∆τ]）。如果ξ和 q 是τ处表面的高度和坡度，则射线在τ处的表面上方，如果ξ₀ +µτ > ξ，则射线在τ+∆τ处的表面上方，如果（ (q−µ)∆τ > (ξ₀ +µτ)−ξ，则射线在τ+∆τ的表面下方。因此我们得到：(46)

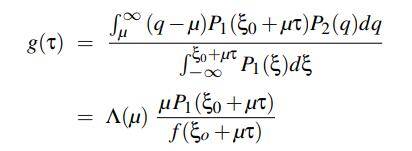
表达式中，f(z)是表面上方的概率 z，Λ是：(47、48)

我们可以通过注意等式 46 中的分子，是其分母的导数来求解等式 45：(49)

然后我们对所有起始高度ξ₀进行积分得到 S(µ)，所有起始微表面高度的平均可见度：(50)

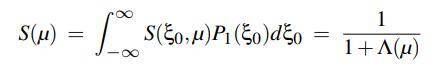
其中，我们使用的 f(ξ₀)的导数是 P₁(ξ₀)
最后，我们添加了一个条件，来检查 v 是否从微表面的正确一侧开始（即侧边一致性），以得到 Smith 单向阴影项:(51)

利用这些方程，我们可以推导出任何微面分布 D 的 G₁（尽管在方程 48 中的积分对某些 D 没有封闭形式的解），同时又与方程 23 一起找到相应的双向阴影掩蔽项。
通常对所有 m 需要执行另一个集成，来获得整个微表面上的平均阴影，但这对于微表面模型来说既不需要也不理想。

参考文献(略)，请下载英文原版文献查看。